Cantor's Miraculous Function

Secular historians often define a miracle (implicitly or explicitly) as the least likely thing to happen. Thus the historian must never use a supernatural explanation for any event. This implies that any secular conception of history must assume an historical continuum: it must be possible to measure the likelihood of a particular event by comparing it to other events we are used to.

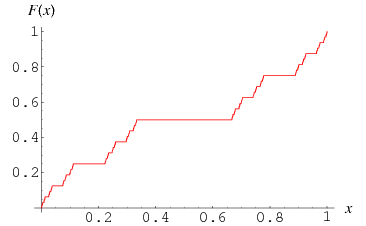
What if there were a simple mathematical illustration showing how those events which have negligible probability, i.e. those events which are by definition the least likely to happen, can have a dramatic effect? In fact, there is, and it has been well-known for quite a long time. It's called the Cantor function and it looks a little something like this:

What's so special about the Cantor function? Here are a few of it's properties. First, it increases continuously from 0 to 1 as x ranges from 0 to 1. Second, it has a derivative defined almost everywhere with respect to the uniform probability distribution (or Lebesgue measure) on the unit interval. Third, this derivative which is defined almost everywhere is zero.

To put it in laymen's terms, pick a random point x in the interval from 0 to 1. The probability is 100% that the Cantor function will be staying perfectly still at that point, i.e. the instantaneous rate of change of the function at the point is zero. And yet! The function increases continuously--that is, without any jumps--from 0 up to 1. (In fact, multiplying by any constant changes none of these properties; the Cantor function could increase as high we like!) This absolutely mystifying property has earned the Cantor function the title "devil's staircase"
by some. I think a more fitting title is this: the Cantor function is a miracle.

Why do I say miracle? Because the event which enables the Cantor function to increase is, in the language of probability, an event which almost never happens. The set on which the Cantor function's derivative is undefined is called the Cantor set. This set meets the historian's criterion of being an event which, by definition, is the least likely event to happen, ever. Yet it is precisely this set which connects this "devil's staircase" from top to bottom. Hence I call this ascension from 0 to 1 a miracle. The historian's explanation will not explain the Cantor function. If one looks at the event most likely to happen, one sees that the Cantor function is not moving. Yet the function moves. Not only does it move--it bridges the entire gap from start to finish, never missing any point between.

The universe is full of such miracles. The continuum is teeming with undetected and undetectable events, whose impact cannot be readily assessed by scientific measurement. Part of the joy of mathematics is discovering such events and bringing them to light! Can there be a more spiritual endeavor?