"Then the Egyptians will hear of it, for in your might you brought up this people from among them, and they will tell the inhabitants of this land. They have heard that you, O Lord, are in the midst of this people; for you, O Lord, are seen face to face, and your cloud stands over them and you go in front of them, in a pillar of cloud by day and in a pillar of fire by night. Now if you will this people all one time, then the nations who have heard about you will say, 'It is because the Lord was not able to bring this people into the land he swore to give them that he has slaughtered them in the wilderness.' And now, therefore, let the power of the Lord be great in the way that you promised when you spoke, saying,
'The Lord is slow to anger,Forgive the iniquity of this people according to the greatness of your steadfast love, just as you have pardoned this people, from Egypt even until now."
and abounding in steadfast love,
forgiving iniquity and transgression,
but by no means clearing the guilty,
visiting the iniquity of the parents upon the children
to the third and the fourth generation.'
Political, philosophical, and theological reflections from a Christian idealist with libertarian leanings and a professional interest in science and mathematics.
Sunday, February 27, 2011
Strength in Numbers
The title of this post is meant as more than just a pun on the title of the Bible's fourth book. It is meant to convey what I think is the key theme of Numbers: a test of strength. The book starts with a census of all military eligible men among the Israelites. It proceeds to continue the narrative begun in Exodus, with the Israelites heading out from Sinai and moving toward the promised land so that they can move in and conquer it. Just as the Israelites are about to enter, the central crisis of the book unfolds. They send spies to scope out the land, and all the spies but Caleb and Joshua come back with an unfavorable report about the gigantic Anakites. Thus the people doubt God's mission for them to enter the land of Canaan, and many try to escape back to Egypt. It is at this moment that God desires to be rid of all the Israelites and start over with Moses, and Moses responds with this plea:
Labels:
Christianity,
God,
numbers,
the Bible,
theology
Thursday, February 24, 2011
Cantor's Miraculous Function
Secular historians often define a miracle (implicitly or explicitly) as the least likely thing to happen. Thus the historian must never use a supernatural explanation for any event. This implies that any secular conception of history must assume an historical continuum: it must be possible to measure the likelihood of a particular event by comparing it to other events we are used to.
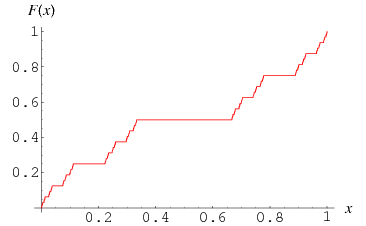
What if there were a simple mathematical illustration showing how those events which have negligible probability, i.e. those events which are by definition the least likely to happen, can have a dramatic effect? In fact, there is, and it has been well-known for quite a long time. It's called the Cantor function and it looks a little something like this:What's so special about the Cantor function? Here are a few of it's properties. First, it increases continuously from 0 to 1 as x ranges from 0 to 1. Second, it has a derivative defined almost everywhere with respect to the uniform probability distribution (or Lebesgue measure) on the unit interval. Third, this derivative which is defined almost everywhere is zero.
To put it in laymen's terms, pick a random point x in the interval from 0 to 1. The probability is 100% that the Cantor function will be staying perfectly still at that point, i.e. the instantaneous rate of change of the function at the point is zero. And yet! The function increases continuously--that is, without any jumps--from 0 up to 1. (In fact, multiplying by any constant changes none of these properties; the Cantor function could increase as high we like!) This absolutely mystifying property has earned the Cantor function the title "devil's staircase"
by some. I think a more fitting title is this: the Cantor function is a miracle.
Why do I say miracle? Because the event which enables the Cantor function to increase is, in the language of probability, an event which almost never happens. The set on which the Cantor function's derivative is undefined is called the Cantor set. This set meets the historian's criterion of being an event which, by definition, is the least likely event to happen, ever. Yet it is precisely this set which connects this "devil's staircase" from top to bottom. Hence I call this ascension from 0 to 1 a miracle. The historian's explanation will not explain the Cantor function. If one looks at the event most likely to happen, one sees that the Cantor function is not moving. Yet the function moves. Not only does it move--it bridges the entire gap from start to finish, never missing any point between.
The universe is full of such miracles. The continuum is teeming with undetected and undetectable events, whose impact cannot be readily assessed by scientific measurement. Part of the joy of mathematics is discovering such events and bringing them to light! Can there be a more spiritual endeavor?
What if there were a simple mathematical illustration showing how those events which have negligible probability, i.e. those events which are by definition the least likely to happen, can have a dramatic effect? In fact, there is, and it has been well-known for quite a long time. It's called the Cantor function and it looks a little something like this:What's so special about the Cantor function? Here are a few of it's properties. First, it increases continuously from 0 to 1 as x ranges from 0 to 1. Second, it has a derivative defined almost everywhere with respect to the uniform probability distribution (or Lebesgue measure) on the unit interval. Third, this derivative which is defined almost everywhere is zero.
To put it in laymen's terms, pick a random point x in the interval from 0 to 1. The probability is 100% that the Cantor function will be staying perfectly still at that point, i.e. the instantaneous rate of change of the function at the point is zero. And yet! The function increases continuously--that is, without any jumps--from 0 up to 1. (In fact, multiplying by any constant changes none of these properties; the Cantor function could increase as high we like!) This absolutely mystifying property has earned the Cantor function the title "devil's staircase"
by some. I think a more fitting title is this: the Cantor function is a miracle.
Why do I say miracle? Because the event which enables the Cantor function to increase is, in the language of probability, an event which almost never happens. The set on which the Cantor function's derivative is undefined is called the Cantor set. This set meets the historian's criterion of being an event which, by definition, is the least likely event to happen, ever. Yet it is precisely this set which connects this "devil's staircase" from top to bottom. Hence I call this ascension from 0 to 1 a miracle. The historian's explanation will not explain the Cantor function. If one looks at the event most likely to happen, one sees that the Cantor function is not moving. Yet the function moves. Not only does it move--it bridges the entire gap from start to finish, never missing any point between.
The universe is full of such miracles. The continuum is teeming with undetected and undetectable events, whose impact cannot be readily assessed by scientific measurement. Part of the joy of mathematics is discovering such events and bringing them to light! Can there be a more spiritual endeavor?
Labels:
Cantor,
history,
mathematics,
science,
set theory,
theology
Tuesday, February 22, 2011
Discontinuity
I read somewhere that the theory of functions had a profound impact on Florensky's philosophy. The assumption of continuity, for him, meant that the philosophy of the modern era was doomed to see everything in purely deterministic terms. The discovery of discontinuity, of functions that do surprising and almost incomprehensible things, signaled for him a turning point. The world was full of wonder again. Learning could be spontaneous, and the mind could leap forward in faith into the unknown.
There has to be something to this. When I teach calculus, I can't help but notice that students have the hardest time processing the definition of continuity--probably because they can't imagine discontinuity. Oh, sure, maybe a function jumps a few times here and there. Or maybe a function like f(x) = 1/x has a vertical asymptote. Big deal. For the most part in my beginning calculus class we deal with functions that are continuous everywhere they're defined, aside from maybe some removable discontinuities.
The definition of continuity is simply that the local behavior of a function f(x) near x = a is the same as the value f(a). The surprising thing to students is that this might not be the case. Take a function like f(x) = x^2, and obviously finding the limit is just a matter of "plugging in" the appropriate value of x. Discontinuity is jarring. It means the function doesn't behave the way one would expect. I find it necessary to hammer this point home for students, because otherwise they'll have a hard time perceiving that continuity is really an issue at all.
There is an intimate relationship between discontinuity and freedom of the will. To construct a continuous function one simply needs a general rule, e.g. f(x) = x^5 - 5. To construct a discontinuous function, one must dissect the continuum, picking out individual points of interest and declaring that a function behave differently at those points. It is this declaration by which a mind exercises its freedom of will. Even if it is silly or strange to do so, I may simply declare that f(5) = 0, even though for every other real number x I say f(x) = 2x. It is an act of will, a bold separation of chosen points from the rest of the continuum, an assertion that my word alone defines what a function is. Its local behavior may be perfectly continuous, and it may have a limit as x approaches 5. I am by no means bound by such trends.
One who is truly skilled at dissecting the continuum can do much more terrible things than making a function with a single point of discontinuity; indeed, it is not hard to define a function which is continuous nowhere, even though it is defined everywhere. I've given my students that problem as an extra credit assignment; I'm asking them to look it up and see if they can explain it to me. They won't be able to produce the example themselves, which is not a reflection on their intelligence so much as on the nature of mathematics. There are certain things one simply cannot imagine unless one has seen.
This is why mathematics is essential to a truly liberal education, and why I find it incredible how many educated people consider math a mere specialization totally closed off even to the average intellectual. There is nothing so liberating to the mind as being able to enter a world of pure thought, a world which is simultaneously the work of our own minds and beyond the mind's control. Every field in the humanities sounds to me to be obsessed with paradigms and paradigm shifts. Mathematics has no such discussions, because there is only one paradigm: discovery through creation. Mathematics is a creative act of will in the purest sense. "Let x be," and it is. What holds most people back from the world of mathematics is their unwillingness to take that leap of faith, to make that bold assumption of creativity, to step out of continuity with the world of the concrete and "practical" (concepts which any intellectual ought to address with suspicion). More than all the scientific applications, more than all the quantitative reasoning and critical thinking skills, mathematics has this one thing to offer the world: intellectual courage.
That is, of course, if one understands it the way, for instance, Florensky did.
There has to be something to this. When I teach calculus, I can't help but notice that students have the hardest time processing the definition of continuity--probably because they can't imagine discontinuity. Oh, sure, maybe a function jumps a few times here and there. Or maybe a function like f(x) = 1/x has a vertical asymptote. Big deal. For the most part in my beginning calculus class we deal with functions that are continuous everywhere they're defined, aside from maybe some removable discontinuities.
The definition of continuity is simply that the local behavior of a function f(x) near x = a is the same as the value f(a). The surprising thing to students is that this might not be the case. Take a function like f(x) = x^2, and obviously finding the limit is just a matter of "plugging in" the appropriate value of x. Discontinuity is jarring. It means the function doesn't behave the way one would expect. I find it necessary to hammer this point home for students, because otherwise they'll have a hard time perceiving that continuity is really an issue at all.
There is an intimate relationship between discontinuity and freedom of the will. To construct a continuous function one simply needs a general rule, e.g. f(x) = x^5 - 5. To construct a discontinuous function, one must dissect the continuum, picking out individual points of interest and declaring that a function behave differently at those points. It is this declaration by which a mind exercises its freedom of will. Even if it is silly or strange to do so, I may simply declare that f(5) = 0, even though for every other real number x I say f(x) = 2x. It is an act of will, a bold separation of chosen points from the rest of the continuum, an assertion that my word alone defines what a function is. Its local behavior may be perfectly continuous, and it may have a limit as x approaches 5. I am by no means bound by such trends.
One who is truly skilled at dissecting the continuum can do much more terrible things than making a function with a single point of discontinuity; indeed, it is not hard to define a function which is continuous nowhere, even though it is defined everywhere. I've given my students that problem as an extra credit assignment; I'm asking them to look it up and see if they can explain it to me. They won't be able to produce the example themselves, which is not a reflection on their intelligence so much as on the nature of mathematics. There are certain things one simply cannot imagine unless one has seen.
This is why mathematics is essential to a truly liberal education, and why I find it incredible how many educated people consider math a mere specialization totally closed off even to the average intellectual. There is nothing so liberating to the mind as being able to enter a world of pure thought, a world which is simultaneously the work of our own minds and beyond the mind's control. Every field in the humanities sounds to me to be obsessed with paradigms and paradigm shifts. Mathematics has no such discussions, because there is only one paradigm: discovery through creation. Mathematics is a creative act of will in the purest sense. "Let x be," and it is. What holds most people back from the world of mathematics is their unwillingness to take that leap of faith, to make that bold assumption of creativity, to step out of continuity with the world of the concrete and "practical" (concepts which any intellectual ought to address with suspicion). More than all the scientific applications, more than all the quantitative reasoning and critical thinking skills, mathematics has this one thing to offer the world: intellectual courage.
That is, of course, if one understands it the way, for instance, Florensky did.
Labels:
Florensky,
free will,
freedom,
mathematics
Monday, February 21, 2011
In defense of not paying attention
Jonah Lehrer writes in an article on the WSJ:
In recent years, however, scientists have begun to outline the surprising benefits of not paying attention. Sometimes, too much focus can backfire; all that caffeine gets in the way. For instance, researchers have found a surprising link between daydreaming and creativity—people who daydream more are also better at generating new ideas. Other studies have found that employees are more productive when they're allowed to engage in "Internet leisure browsing" and that people unable to concentrate due to severe brain damage actually score above average on various problem-solving taskI'm glad there's someone out there to justify my blogging/web-browsing habits while I'm trying to work on my research.
Labels:
distractions,
research,
thinking outside the box
Sunday, February 20, 2011
Evolution of Science and Religion
Some people argue that science has its place, and religion has its place. But this perspective fails to take into account evolution, specifically in culture and language. Consider the concept of (not to mention the word) "science." Once theology was the queen of the sciences, since "science" in this sense meant simply the acquisition of knowledge. "Natural science" is what most people now think of as "science," but even then it is not so easy to think of a definition. Is it a method? Is it a body of knowledge? Is it knowledge about particular kinds of things? Which things? Can it imply a certain kind of "worldview"? Or consider the word "religion." How does one define it? Does it have to involve belief in the supernatural? Does it have to involve participation in an institution of the faithful? Is it a philosophy? Is it a collection of morals? The difficulty of these questions is symptomatic of a deeper fact, namely that the word "religion," like the word "science," has a long cultural and linguistic history which is still moving forward. I find it highly absurd to think that we could predict the outcome of this evolution for a period of time longer than a few years.
Application: Anyone interested in providing a view on the relationship between religion and science must in some sense offer definitions of those terms. Yet these definitions must compete with one another for popular usage, and thus they are hardly definitive. For instance, science as a worldview has gained some ground in the intelligentsia at certain points in recent history, but it probably will not have huge success in the long run. It feels to me as if the most popular definition of science these days is strictly utilitarian: we like it because of what it does for us. For that reason our culture has little reason to precisely sort out the relationship between science and religion; as long as science just keeps giving us cool stuff, can't we all just believe what we want? There are probably much worse ways our culture could handle the situation. In any case, we cannot simply decide what the two words "science" and "religion" mean, and then logically deduce their compatibility. If we did that, then all of language would just be mathematics.
Application: Anyone interested in providing a view on the relationship between religion and science must in some sense offer definitions of those terms. Yet these definitions must compete with one another for popular usage, and thus they are hardly definitive. For instance, science as a worldview has gained some ground in the intelligentsia at certain points in recent history, but it probably will not have huge success in the long run. It feels to me as if the most popular definition of science these days is strictly utilitarian: we like it because of what it does for us. For that reason our culture has little reason to precisely sort out the relationship between science and religion; as long as science just keeps giving us cool stuff, can't we all just believe what we want? There are probably much worse ways our culture could handle the situation. In any case, we cannot simply decide what the two words "science" and "religion" mean, and then logically deduce their compatibility. If we did that, then all of language would just be mathematics.
Labels:
evolution,
mathematics,
science and religion
Wednesday, February 16, 2011
Proof that God loves us and wants us to be happy...
Labels:
awesomeness,
cookies
Tuesday, February 15, 2011
This misnomer of "self organizing" systems
The study of self organizing is extremely important in modern science, whether in evolutionary biology, economics, or even the physical sciences. I once went to a talk on the study of self-organizing systems in the context of crime syndicates in Los Angeles. There are even some interesting applications at the basic level of image segmentation: mathematicians working in nonlinear analysis are now able to devise computer algorithms to detect different parts of a photograph using evolutionary partial differential equations. There is a key idea encompassing all of these fields of research: complex systems can "organize themselves" not according to a preset plan, but according to certain rules, with certain types of organization being "selected" over others. For instance, in image segmentation, it would be pointless to try to give a computer all the necessary preset criteria for identifying a piece of an image in a photograph. (How do you know where a mountain ends and a sky begins? Try writing down the exact criteria just to see how impossible this is.) Instead, if you give a computer general rules (dictated by a PDE) by which to allow its image segmentation to evolve, eventually an appropriate segmentation will be selected.
So why do I say "self organizing" is a misnomer? The argument can be put pretty simply in a mathematical framework. A self organizing system is nothing more and nothing less than a dynamic system. Let x(t) by the state of a system at time t, with the state space given by H, and let f be a function. Then we can write x'(t) = f(x(t)) for given initial data x(0) in H, where x' is the time derivative of x. This defines a dynamic system. For discrete time, we can simply write x(n+1) = f(x(n)). The long-time behavior of a dynamic system is, in a completely literal sense, the result of evolution. The crucial point is this: this behavior is governed by the function f. It would be absurd mathematically and otherwise to say that x(t) determines itself. On the contrary, it is clearly determined by f, over which it has no control. (I could mention stochastic dynamic systems, but the same principles apply there as well; randomness does not mean the system is somehow freer.)
So why do I say "self organizing" is a misnomer? The argument can be put pretty simply in a mathematical framework. A self organizing system is nothing more and nothing less than a dynamic system. Let x(t) by the state of a system at time t, with the state space given by H, and let f be a function. Then we can write x'(t) = f(x(t)) for given initial data x(0) in H, where x' is the time derivative of x. This defines a dynamic system. For discrete time, we can simply write x(n+1) = f(x(n)). The long-time behavior of a dynamic system is, in a completely literal sense, the result of evolution. The crucial point is this: this behavior is governed by the function f. It would be absurd mathematically and otherwise to say that x(t) determines itself. On the contrary, it is clearly determined by f, over which it has no control. (I could mention stochastic dynamic systems, but the same principles apply there as well; randomness does not mean the system is somehow freer.)
Saturday, February 12, 2011
Real reality
I watched Inception for the second time last night and loved it every bit as much as the first time. The great thing about sci-fi movies like that is their ability to ask deep questions in an entertaining way. The question that came to mind last night was, How do we know what's real? And do we really care?
Spoiler Alert: Skip the next paragraph if you haven't seen the movie, since it will ruin it for you.
When Cobb and his wife Mal are lost together in a dream world of their own making, Cobb realizes that eventually they need to wake up. But Mal has left the real world behind, and the only way to get her to go back is to implant an idea in her mind--the idea that this life she's living isn't real. From within the dream world, only death can cause a person to wake up. So Cobb has to implant in her subconscious mind the idea that they must escape this world through death. The plan works, only too well. After they commit suicide in the dream world, they wake up in the real world; only Mal hasn't lost the idea planted in her mind. She refuses to accept the world around her as real. She insists that the two of them still need to wake up. This leads to a second suicide--only this time she is gone, never to wake again.
Spoiler Alert: Skip the next paragraph if you haven't seen the movie, since it will ruin it for you.
When Cobb and his wife Mal are lost together in a dream world of their own making, Cobb realizes that eventually they need to wake up. But Mal has left the real world behind, and the only way to get her to go back is to implant an idea in her mind--the idea that this life she's living isn't real. From within the dream world, only death can cause a person to wake up. So Cobb has to implant in her subconscious mind the idea that they must escape this world through death. The plan works, only too well. After they commit suicide in the dream world, they wake up in the real world; only Mal hasn't lost the idea planted in her mind. She refuses to accept the world around her as real. She insists that the two of them still need to wake up. This leads to a second suicide--only this time she is gone, never to wake again.
Friday, February 11, 2011
Abstract thought in applications
Sitting here in Para Coffee grading my students' first exam of the semester. It's not going so well, or at least not as well as I'd hoped. I feel like the last time I taught this course my students were a little more prepared for calculus. I guess what I have to remember is that this is spring term--a chance for those who really hate math to get this class out of the way. Oh boy.
As I grade, I'm realizing how silly it is when we break things down into "abstract" and "concrete." In math, solving concrete problems takes abstract thought--that's the whole point of even learning this stuff. You need to build something with a given amount of material and optimize the amount of space it contains. You need to maximize the speed of your vehicle. Whatever. The point is that if you just attacked the problem with no abstract thought whatsoever, you'd be stuck. If you can't imagine the problem as anything other than what it looks like on the surface, you can't solve it.
The real distinction, in my opinion, is between abstract and habitual. Students hate word problems. Why? Because they don't always look the same as every other problem they've ever done. They actually have to approach the problem on its own terms. That's frustrating, and students commonly express the opinion that their teacher "never gave us anything like this before." Students can do habitual assignments pretty well. It's much harder to get them to actually solve a problem. That's why they'd prefer to just take a bunch of meaningless limits and crank out a number or a "DNE" (does not exist) than solve real problems that someone in real life might actually ask. I worry about the implications for their future occupations. Will they be stuck just doing the same task over and over again, simply because that's easier? I suppose there's nothing wrong with that. It's just that you'd think a UVA student might imagine something more. I don't know.
The problem is that students have a hard time seeing the heart of a problem. They don't want to sit down and think about principles. It's so easy to treat everything mechanically. Yet it's so much easier to actually solve a problem by first figuring out what in the world they're looking for. And yes, that means abstractly. For instance, if you're looking for area, write down area = length times width. This is a thoroughly abstract statement, but it gives you a guide to solving the problem. You can't approach a concrete problem and solve it without identifying the abstract principles governing it. Indeed, one's knowledge of the abstract is tested best in application questions.
That's it for now--just a short rant on the difficulties of teaching math. I admit I can't help like feeling that my students' failure is my failure, even though that's absurd. I'm just some grad student the school throws up in front of these kids for less than three hours a week. Most of what these students need to know, there's no way I can teach them in three weeks before their first exam.
As I grade, I'm realizing how silly it is when we break things down into "abstract" and "concrete." In math, solving concrete problems takes abstract thought--that's the whole point of even learning this stuff. You need to build something with a given amount of material and optimize the amount of space it contains. You need to maximize the speed of your vehicle. Whatever. The point is that if you just attacked the problem with no abstract thought whatsoever, you'd be stuck. If you can't imagine the problem as anything other than what it looks like on the surface, you can't solve it.
The real distinction, in my opinion, is between abstract and habitual. Students hate word problems. Why? Because they don't always look the same as every other problem they've ever done. They actually have to approach the problem on its own terms. That's frustrating, and students commonly express the opinion that their teacher "never gave us anything like this before." Students can do habitual assignments pretty well. It's much harder to get them to actually solve a problem. That's why they'd prefer to just take a bunch of meaningless limits and crank out a number or a "DNE" (does not exist) than solve real problems that someone in real life might actually ask. I worry about the implications for their future occupations. Will they be stuck just doing the same task over and over again, simply because that's easier? I suppose there's nothing wrong with that. It's just that you'd think a UVA student might imagine something more. I don't know.
The problem is that students have a hard time seeing the heart of a problem. They don't want to sit down and think about principles. It's so easy to treat everything mechanically. Yet it's so much easier to actually solve a problem by first figuring out what in the world they're looking for. And yes, that means abstractly. For instance, if you're looking for area, write down area = length times width. This is a thoroughly abstract statement, but it gives you a guide to solving the problem. You can't approach a concrete problem and solve it without identifying the abstract principles governing it. Indeed, one's knowledge of the abstract is tested best in application questions.
That's it for now--just a short rant on the difficulties of teaching math. I admit I can't help like feeling that my students' failure is my failure, even though that's absurd. I'm just some grad student the school throws up in front of these kids for less than three hours a week. Most of what these students need to know, there's no way I can teach them in three weeks before their first exam.
Labels:
abstract thinking,
mathematics,
teaching
Wednesday, February 9, 2011
What is "intelligent"? What is "design"?
If you read my posts on a regular basis (I really have to wonder how many of you there are) you may have noticed that I keep coming back to two seemingly abstract subjects: epistemology, and the philosophy of mind. These seem to creep up on me as an unavoidable subtext to just about every debate I care about: between Christianity and atheism, concerning the origins of life and the material world, and even on bioethics. Nowhere has this been more true than in the debate concerning evolution that seems to go on relentlessly. I've been part of a reading group on Francis Collins' book, The Language of God, in which he lays out a case for Christianity with a special emphasis on harmony between faith and science. The reading group involves Christians and atheists/agnostics of various backgrounds, and I've appreciated the chance to clarify some of the key issues. The key issues are, in my opinion, all matters of epistemology.
Labels:
atheism,
Christianity,
evolution,
God,
intelligent design,
science and religion
Monday, February 7, 2011
Materialism and the Mind
Christianity has historically embraced a dualist interpretation of the mind/body problem inherited largely from the Greeks (Plato, Aristotle, etc.). There are two main reasons for this embrace: the first is explanatory, and the second is ontological. The explanatory power of dualism is intuitive to many (if not most) people. Thought does not appear to be physical, and reason appears to ascertain truths far more abstract than any material substance. It seems intuitively plausible that reason itself must be the product of a non-material substance. Along these lines an even more compelling case can be made for the non-physical existence of the will, which, if separated from the mind, constitutes perhaps yet a third "substance" in addition to the mind and the body. The ontology of dualism (or trio-ism?) is probably even more important to the Christian than this explanatory power. It typically helps explain the image of God in man, the ability for human beings to spiritual, and the significance of human life over and against plant and animal life.
Labels:
dualism,
epistemology,
God,
materialism,
philosophy,
theology
Thursday, February 3, 2011
Did we really expect anything different?
Planned Parenthood is an organization whose moral compass is so totally backward that its employees can look directly at the bloody corpse of an aborted fetus and not repent. Is it really any wonder that its employees would see nothing wrong with an underage sex ring?
Labels:
abortion,
Planned Parenthood
Wednesday, February 2, 2011
Data, the comedian
He's probably funnier than most of the scientists who know how he works.
Labels:
robots,
science,
technology
Tuesday, February 1, 2011
Two bioethics issues with one story
A helpful article from LifeNews.com: "Babies Can Be Treated With Adult Stem Cells, Even in the Womb." As the title suggests, this report outlines a few ways in which scientists are using adult (not embryonic) stem cells to treat children of a young age, even unborn children.
Two things: First, the more the public realizes the advantages of adult stem cell research, hopefully the less we will support the destructive kind of embryonic stem cell research. They really are two very different things.
Second, I wonder how long we can live with the moral tension created by the ability to both save and destroy life in the womb. In a world where it's possible to cure defects in children still in the womb, how much longer will we really believe it's okay to kill these same children?
Two things: First, the more the public realizes the advantages of adult stem cell research, hopefully the less we will support the destructive kind of embryonic stem cell research. They really are two very different things.
Second, I wonder how long we can live with the moral tension created by the ability to both save and destroy life in the womb. In a world where it's possible to cure defects in children still in the womb, how much longer will we really believe it's okay to kill these same children?
Labels:
abortion,
bioethics,
stem cells
A Church sign worth reading
Labels:
church signs,
failblog
Subscribe to:
Posts (Atom)